Back to Table of Contents
Robert Xiao won the contest with the following submission:
First, the algorithm from the Lisp listing on The Agrippa Files:
It is a very straightforward in-house "encryption" algorithm that encodes data in 3-byte blocks. The design is clearly ad-hoc, and it does not reflect any known public cryptosystem; in particular, the reference to DES has nothing to do with the actual DES cryptosystem (the un-make-des function more closely resembles the RSA algorithm). This algorithm encodes data in 3-byte blocks. First, the 8 bits in each byte are permuted through a 8-position permutation ("do-it"), then the bits are split into two 12-bit integers (by taking the low 4 bits of the second byte and the 8 bits of the first byte as the first 12-bit integer, and the 8 bits of the third byte and the 4 high bits of the second integer as the second 12-bit integer). Each is individually encrypted by taking them to the 3491th power, mod 4097; the bits are then reassembled into 3 bytes.
[Side note: 3491 appears nowhere in the code, but it is the exponent which reverses the action of taking the 11th power, mod 4097 (the implementation of un-make-des); that is, taking a number to the 3491th power mod 4097, then to the 11th power, again mod 4097, will result in the original number (mod 4097) for most integers. (This doesn't work for numbers divisible by 17 or 241; evidently, the developer never ran into such values when using his encryption system as they would otherwise corrupt the text).] [Editor's Note: While the mathematics of RSA cryptography are somewhat beyond the editor's, the supposition that 17 and 241 (the two prime factors that when multiplied are the public modulus) are somehow problematic appears to be incorrect. Ayal first pointed me to this possible error, and secondary corroboration appears to bear this out.]
The 8 bits of the middle byte are permuted through a different 8-position permutation ("do-too-it") and the three bytes are output as encoded bytes. The big block of data is the whole poem encoded with this algorithm and printed as MacRoman characters (with escapes, e.g. 0x5c, the slash character, is output as \\). Sadly, a combination of font and printing limitations means that the printout is not enough to directly decode the poem: several characters are unprintable (and so are "invisible" in the printout), there is no way to reliably distinguish tabs (0x09) from spaces (0x20), and some characters have been printed incorrectly by the font (e.g. the "e" in the repetitive " e\\ sequences should actually be an e with a circumflex (ê), but the printout doesn't show this). Consequently, the poem can't be completely recovered from the printout, but I am confident that the analysis is correct.
Note that the design of this algorithm ensures that any particular (aligned) block of 3 characters will encrypt the same way, since each block of 3 characters is independently encrypted. Thus, it exhibits a number of cryptographic weaknesses, primarily exhibited as regular patterns due to repeated text in the original plaintext.
A few sample encryptions (also shown in figure [Encrypted Samples] in case the gibberish below gets corrupted in transit):
The encryption of three consecutive spaces is " ê\" (quotes added for clarity); since repeated spaces appear very often (e.g. before each chapter marker), this sequence can be seen repeated often.
The encryption of
tonight red lanterns are battered, laughing, in the mechanism.(the last few lines of the poem) is
ΣÑÀQ$£¿Ì[ıƒ^ü…ïÓ êÊyMIÇ…~/ôì≈^Èür˙Q¯(ÀA}|yÙ¥3W+£¶ò∆©«ò\which again matches the last few characters in the data block of the Lisp program listing.
Next, the program:
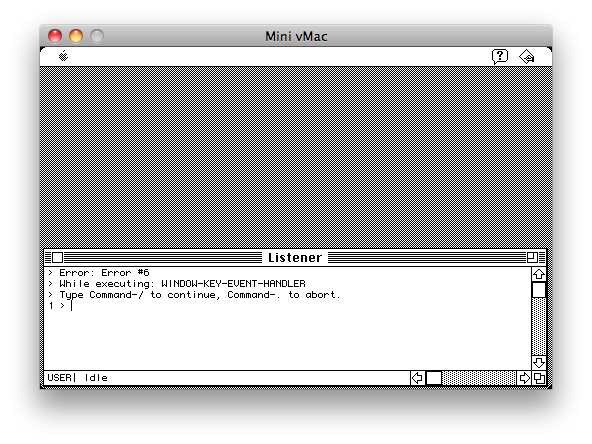
The first major observation I made was that the application was compiled with a version of Macintosh Allegro Common Lisp dating back to 1989, possibly version 1.2.2 or 1.2.3. The application contains a bug which allows users to enter the Lisp REPL, a fully-featured interactive environment in which the code and data of the program can be directly manipulated. To exploit this bug, all you have to do is press some keys on the keyboard when the very first (empty) window appears. The bug is caused by a missing keyboard entry handler in that window; hitting keys on the keyboard should trigger the missing handler and result in an error. Upon any errors, the Lisp interpreter is configured to start its REPL, shown in figure [Listener].
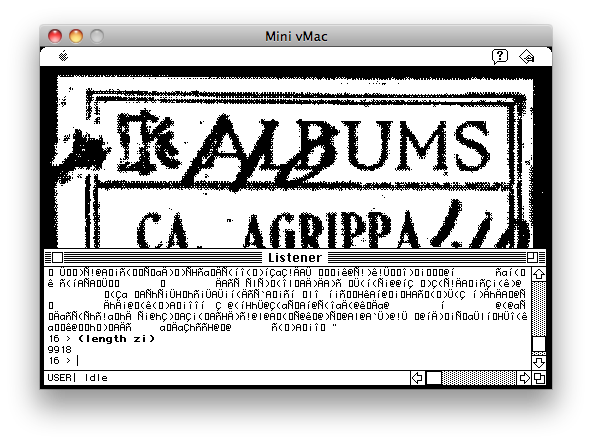
Exploiting this bug allows us to examine the program's execution in much more detail than was previously possible. First, to get a mouse cursor, enter (_ShowCursor) at the prompt (with the parens and the underscore). Editing becomes easier after that. Typing (lisp-implementation-type) gives "Macintosh Allegro Common Lisp", as expected. To get a list of *every* variable defined, type (apropos-list ""). This takes a long time to run; I've attached the last part of this dump as figure [Symbols]. You can see some unusual names at the end, like "shoot-gun", "*mingzi*", "*about-agri*", etc. (note that Lisp is not case-sensitive with its symbol or variable names). In fact, all variables after *TRACE-OUTPUT* are variables from the Agrippa program. Examining the Lisp code from the Agrippa Files, we see that many of the variable names are the same, but not all are. This immediately suggests that some variables were renamed, added or removed during the process of software development, implying that the Lisp listing was for an earlier pre-release version of the program.
The function "UN-ROLL-ZI" is suspicious, as it mirrors the name of "un-roll-the-text" in the original Lisp listing (in fact, "zi" means "words" in Chinese; a few variable names are named in languages other than English). However, the "zi" variable is not currently available. If you start the program again (from a fresh disk image, i.e. "for the first time"), and press keys when the poem window appears, typing in "zi" at the REPL will yield the complete, original text of the poem.
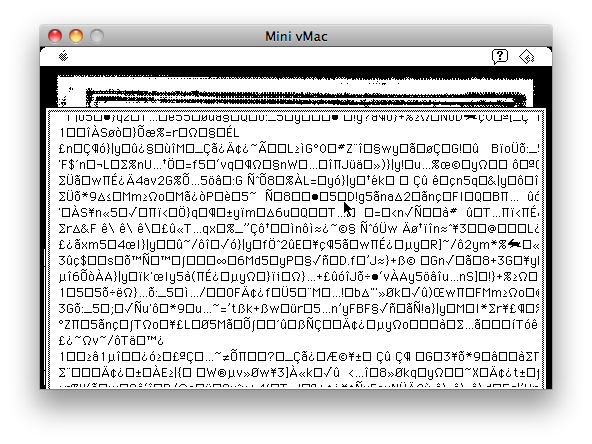
However, we are interested in establishing whether the encryption algorithm used to store "zi" in the Lisp program is the same as the one used in the older Lisp listing. In our original REPL, it turns out that the variable "cl" has the value 3, the same as the "cell-length" variable in the original listing. If we set "cl" to some other value, we can skip the decryption routine, allowing us to see the original "encrypted" data. I set cl to 10000 (larger than the poem itself), then used (continue). Agrippa dutifully begins to scroll a mountain of encrypted gibberish (figure [Encrypted]), and we can see the telltale " ê\" sequence in this screenshot. I can actually confirm that the decryption algorithm used in the Agrippa binary is functionally identical to the one implemented in the Lisp listing, i.e. that part of the program did not change between that listing and the final shipped version of the program. Therefore, the major mystery of "what encryption algorithm was used" has been solved.
There are a few more things to resolve:
I) Scanning the binary for these encrypted strings turns up absolutely nothing. The reason is that the Macintosh Common Lisp compiler compresses the main program code into the executable, then fishes it out and decompresses it during startup. So, string searching will not turn up anything. The best bet if you want to get the encrypted mass of text is to use Linux ckpt or a similar tool to get a memory dump of Mini vMac after the Agrippa program has been loaded. The compression is not in any way a form of encryption, so we won't discuss it in depth.
II) What's that mass of "encrypted" text that gets printed out at the end? To be honest, I'm not 100% sure. However, from my observations I can tell it contains around 40 unique (printable) symbols, far short of the 96 one would expect to see for a properly encrypted piece of text (as an example, the original encrypted text has a lot more unique symbols compared to the garbage shown at the end). From experimentation, I suspect that the text is generated by applying the decryption algorithm again to the plain text to reduce it to gibberish (see Figure [Re-encrypted] for an example of some gibberish generated in this way). [Editor's note: See Robert's follow-up below.
III) Why doesn't the program run again the second time? This one's pretty easy: the program corrupts itself at startup. Originally (as indicated in the Lisp program listing), the plan was to just write 40000 0xff bytes to the binary ("trash"), which would inevitably render the program "corrupt". At some point, someone clearly thought it would be more artistic to use a "genetic code", so the final version writes 6000 randomly-chosen (but fixed) As, Cs, Gs and Ts to a particular spot in the application file. This corrupts several routines in the program, preventing it from starting or running normally (or, depending on the computer used, freezing or crashing the whole system). Note that the genetic code has a codon entropy of 5.97 bits/codon, much higher than any natural DNA sequence known (they top out at around 4-5 bits/codon), and a BLAST nucleotide search turned up no results. It is therefore likely that it is randomly selected (or matched against an artificial DNA sequence, e.g. the sequence shown in the book). [Editor's note: see Nikita's submission and implementation of this routine, demonstrating that it is a RNG using a fixed seed, and therefore "fake" genetic code.
Attached images:
Then Robert further attached a complete dump of the emulator memory, and provided an implementation of the decryption algorithm in Python (with the zi variable being extracted to a separate data file).
Later still, Robert provided this further information:
As a little bonus, I can now explain exactly how the "encrypted" text scroll is generated.
The plaintext poem is simply fed through the "un-waymute-it" (upp-it) function line-by-line, character-by-character, which effectively implements a simple substitution cipher over the characters. The characters are thus modified to become unrecognizable, but the encryption is trivially reversed by putting the text through "waymute-it". Unfortunately, due to the limitations of the text display in the program, it is impossible to precisely determine the ciphertext (since some characters are replaced with boxes, and others are missing entirely); thus, "decrypting" the ciphertext that scrolls at the end is impossible to do precisely. However, since it's a simple substitution cipher, the characters that are readable can be used to reconstruct at least part of the text.
As a demonstration, I've attached a modified version of my previous robert.py program which implements the substitution cipher and demonstrates a partial "decryption" of the readable parts of the first page of scrolled ciphertext.
As before, it starts by decrypting zi.dat and printing the original poem (therefore, it needs zi.dat to function, which I've re-attached here for convenience). It then prints out several pages of ciphertext. You can compare the generated encrypted text with the text that is scrolled during the last 25 seconds of the "agrippa-emulation.mov" movie on The Agrippa Files to see that the implemented encryption routine matches the original. Note that the last line of ciphertext on each "page" is not visible due to the limited height of the text display window. Finally, the script prints out a partial decryption of the first page of ciphertext based on what is visible (boxes have been replaced with • characters, which decrypt to <).
Robert Xiao can be contacted at .